World Puzzle Championship

The organizers of the 9th WPC thank the puzzle and game manufacturers who donated their products for use during the WPC.

This year's competition was highlighted by an unprecedented variety of puzzles on paper. Of course, this is the direct result of the ingenuity of the puzzle designers. Thanks go to all who contributed.

Of particular note is the extraordinary support from Erich Friedman, who contributed 18 separate puzzle designs. This includes the Multi-Level Rolling Block Maze featured in Part III, and 10 of the 13 Battleship puzzles presented in Part V. Thank you, Erich!

Adrian Fisher	Roundabout (IV.2), Chasm Maze (VII.13)
Alexey Pajitnov	Square Re-construction (I.17)
Craig Kasper	Railroad Track(I.18), Gridlock(I.19), Weighted Battleships (V.9), Stepping Stones (VIII.6)
Dave Tuller	ABC Connect (I.7), Rectangles (I.12), Tents (I.14), Spokes (VIII.7), Black&White (VIII.8), Eminent Domain (VIII.10), Lay Bricks (VIII.12), Fences (VIII.18)
Ed Pegg, Jr.	Times 4 (I.6), Crossword Maze (VII.2)
Erich Friedman	Distance (I.9), Balancing Act (I.10), Rolling Block Maze (I.15), Multi-Level Rolling Block Maze (III), Non-rounded Battleships (V.2), Squared Battleships (V.3), Minesweeper Battleships (V.5), Ship Battleships (V.6), Easy as Battleships (V.7), Crowded Battleships (V.8), Retrograde Battleships (V.10), Either/Or Battleships (V.11), Diagonal Battleships (V.12), Hexagonal Battleships (V.13), Numerical Jigsaw (VIII.1), Do or Die (VIII.9), Equations (VIII.14), Hexasperation (VIII.19)
Fred Piscop/Will Shortz	Russian Cross (VIII.16)
Goh Pit Khiam	Stealth (IV.3)
Mark Gottlieb	Mr. Potato Head (VI.1), Hawaiian Holiday (VI.7), Playground (VI.8), Block Party (VI.12)
Mark Rosewater	Die Cast (VI.4), Work Product (VI.5)
Michael Rios	Alternate Corners (I.3), Symbolic Dominoes (I.20), End View (VIII.2), RecTangles (VIII.4), Number Place (VIII.17)
Michael Selinker	Placement Test (VI.9), Olympic Spirit (VI.10)
Moshe Rubin	Battleships (V.1)
Nancy Schuster	Friday the 13th (I.1)
Nick Baxter	Broken Mirror (I.5), Overlay (I.8), Lunar Lockout (II.1,2,4), Zome K6 (IV.4), Connect-i-cut (VII.3), Board Stiff (IX.1), Triangle Count (IX.2), CONN Tour (IX.3), Vantage Point (IX.7), Cube Patterns (IX.8)
Nob Yoshigahara	Tri-Dissection (VIII.15)
NOBrain Corp	Lunar Lockout (II.3,5,6; IX.4)
Paul Peterson	Paint by Numbers (VI.6)
Peter Grabarchuk	Cut the Q (I.4)
Richard Garfield	Balloon Balance (VI.2), Dungeon Escape (VI.3)
Scott Kim	Triangles (VII.1), Viewpoint (VIII.5; IX.6)
Serhiy Grabarchuk	Sliding Pyramid (IV.1), Tangram Battleships (V.4)
Sherlee Oldacre	Paint It Black (I.16)
Simon Nightingale	3-D Paint by Numbers (Instructions)
Teeuwynn Woodruff	Character Study (VI.11), Hidden Puzzle (VI.13)
Will Shortz	Common Touch (I.2), River Crossing (I.11), Next! (VIII.3), Gold Medal Boggle (VIII.11), Cartoon Sequence (IX.5)

The 9th World Puzzle Championship--Back in the USSA
Article for Spring 2001 Games World of Puzzles

The 9th World Puzzle Championship returned to the United States for the first time since its inception in 1992. And what a homecoming it was. The host US team was hospitable in every way, except when it came to dispatching the competition--running away with the team title for the third year in a row.

After two days of renewing old friendships, making new acquaintances, and sightseeing in New York City, the contestants settled down and got to the business at hand: solving puzzles! After two long, grueling days of competition, 4-time champion and favorite Wei-Hwa Huang gained an impressive lead over the rest of the field. However, it's never over until it's over; and this year, organizers added a final playoff round to put an exclamation mark on the individual championship.

The top 10 individuals going into the final playoff round were handicapped based on their point score. 10th place received 30 minutes to solve the 8 problems, with 1st through 9th receiving proportionately more time, based on the points earned during the previous rounds. Aside from the time handicap, the scores from the previous rounds were ignored in determining the rank of the top 10 individual places.

Despite an intimidating 11 minute head start on the rest of the field, Wei-Hwa Huang made one miscalculation that he did not notice and correct until just 2 minutes remaining in the round. This opened the door for German Ulrich Voigt, who calmly ignored his 15 minute disadvantage and solved each problem correctly, finishing his last problem with just over 4 minutes remaining in the round. The 2 minutes, 11 second difference made Ulrich the first new champion in 4 years.

Also among the top 10 finalists were US team members Zack Butler (6th) and Ron Osher (9th), and Canadian Derek Kisman (7th).

The competition events concluded with a museum exhibit of jigsaw and mechanical puzzles hosted by puzzle experts Anne D. Williams and Jerry Slocum, and a festive awards dinner at the home of US Team member Ron Osher.

The following pages contain some of our favorite puzzles from the competition, designed by some of the best puzzle and game designers from around the country. We hope you enjoy their puzzles as much as we have. We would also like to acknowledge the companies that donated products used during the competition: Binary Arts, Wizards of the Coast/Hasbro, and Zometool; our online host: PuzzleTime.com, and longtime sponsor: Random House.

The 10th World Puzzle Competition will be in the Czech Republic later this year. Open qualifying to select some members of the US and Canadian teams will be held on Saturday, June 9. Visit the US Team web site at www/puzzles-usa.org for details.

Selected Puzzles from the 9th WPC
Published in the World Puzzle Federation Newsletter

I'd like to present an overview of the puzzles used from the 9^th World Puzzle Championship last year, highlighting those that I think are the most interesting. Actually, I think ALL the puzzles were interesting in some way or another, otherwise I would not have included them in the competition! So please don't be too disappointed if I did not include your favorites here.

For Part I, we tried to lighten up the first round of competition with a little bit of fun. Since the first day was Friday the 13^th, this was an obvious theme to use for a few of the puzzles. The most obvious example was the very first puzzle: a word-search using the names of movie stars appearing in the Friday the 13^th horror film series. (since the movies were so bad, these actors and actresses have never been heard from again, so the rules of culture-neutrality didn't apply!)

This puzzle is a little scarier than the normal word search: we've left out one of the 36 first and last names, and ask you to figure out which one is missing!

AMY STEEL	KEVIN BLAIR	RON PALILLO
BARBARA BINGHAM	KIRSTEN BAKER	SHAVAR ROSS
BRUCE MAHLER	LARRY ZERNER	STU CHARNO
CAROL LACATELL	MARK NELSON	SUSAN BLU
DANA KIMMELL	PAUL KRATKA	TONY GOLDWYN
JOHN FUREY	RICHARD YOUNG	TRACIE SAVAGE

"Logic grids" have become a staple of the WPC, and a number of styles have become recurring favorites. So it's always refreshing to see a new, innovative style appear, which sums up my enthusiasm for the Railroad Track puzzle.

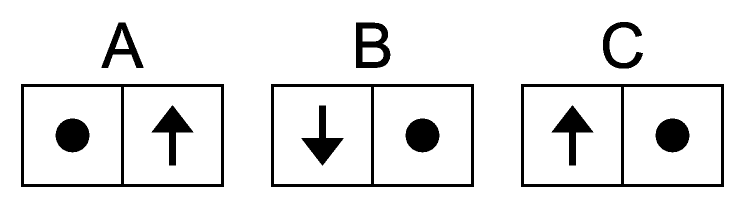
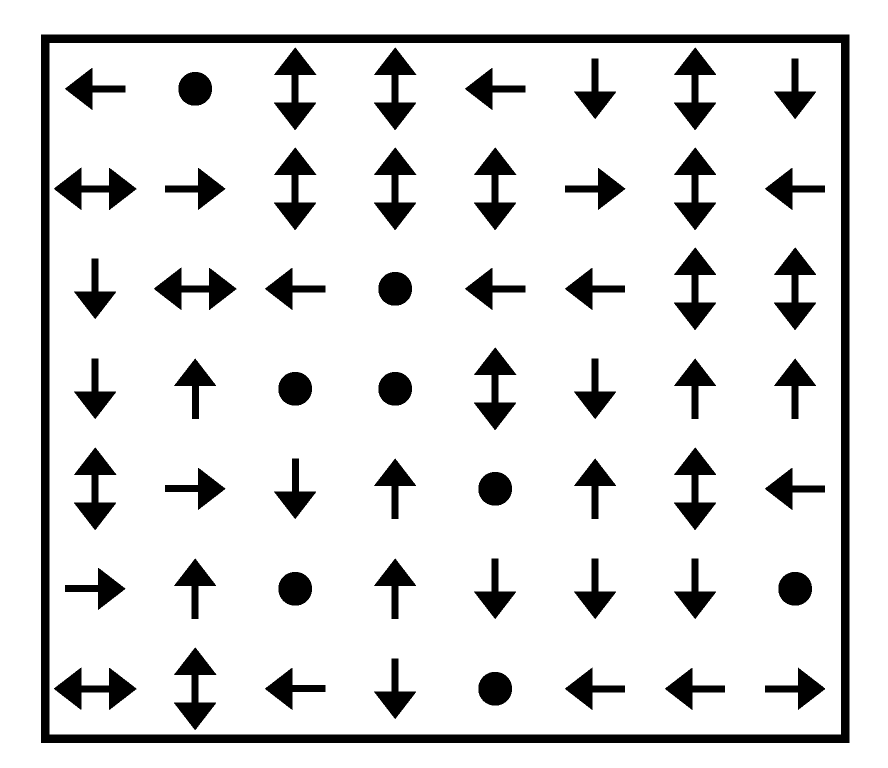
The Instruction Booklet and the pre-competition rules meetings are important parts of keeping the competition fair for everyone. The authors and editor must strike a delicate balance between giving enough information ahead of time so the that puzzles will be readily understood, and not giving too much information so that the puzzle could be solved ahead of time.

Symbolic Dominoes was a case where we gave away too much information. The puzzle was actually a two-part puzzle in disguise. The first part was to determine the set of dominoes; only then could you begin to solve the second part and actually locate them in the grid. Of course, my hope was that people would have to discover the unique set of dominoes during the competition. But unfortunately, this challenge became obvious during rules meeting, and I think that most smart solvers discovered the tricks the night before.

If nothing else, I recommend that you at least determine the complete configuration of the unusual set of dominoes in the problem below.

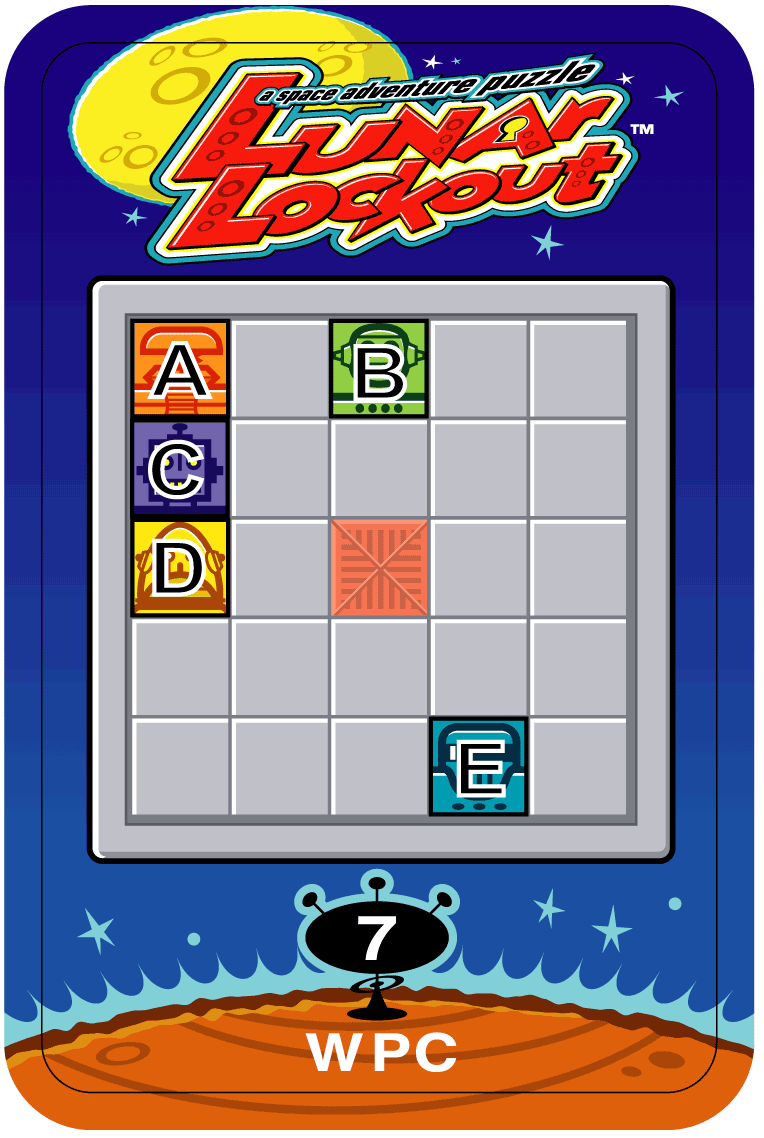
Part II was a speed round featuring the Lunar Lockout game. The US Team first saw this puzzle type (then known as UFO) in the 1999 U.S. & Canadian team qualifying test, and then again during the 2000 qualifier. It was originally designed by Nob Yoshigahara as a paper puzzle, but Binary Arts quickly saw the commercial potential, and eventually produced the game. They were also generous enough to give the game to each of the competitors so that all solving could be the with physical model rather than on paper (which is a LOT harder to do--just ask the US team!)

The puzzles appear to be easy, but they are not. I like to describe them as a maze where the barriers move along with your pieces, but the complexity is surprisingly more profound than that.

This section originally wasn't a timed event, and included one additional puzzle. Mercifully, we changed our minds, and removed the hardest (and most unique) of the puzzles. So that no one is deprived of the experience, I include it here.

Unfortunately, I would not do justice to the physical and manipulative puzzles used in Part III and Part IV if I reproduced them here. So I won't try. These sections included a representative cross section of popular styles (sliding block, maze, edge-matching, 2D tray, and 3D geometric assembly), and were carefully designed and selected to reward deduction, not trial-and-error or luck. The typical WPC participant is not as experienced with these types of puzzles, so the scores were down, particularly for Part IV. Regardless, I hope that future WPC organizers share my view of the importance of these puzzle styles, and will continue to include manipulative puzzles in the competition.

I really like puzzles that combine different themes together into a good new design. The Battleship style is ripe for this, as we saw in Budapest with Battleship Varia. For Part V, we continued this theme by using Erich Friedman's large collection of new variations.

However, the big surprise for me was Serhiy Grabarchuk's Tangram Battleship -- a beautiful combination of the classic manipulative puzzle design and one of the WPC's all-time favorite puzzle styles. The triangular shapes are very unusual, making the puzzle a little more difficult because the solver must be very careful to make sure that ships don't touch at a single point (and at the same time must remember to take advantage of this restriction!).

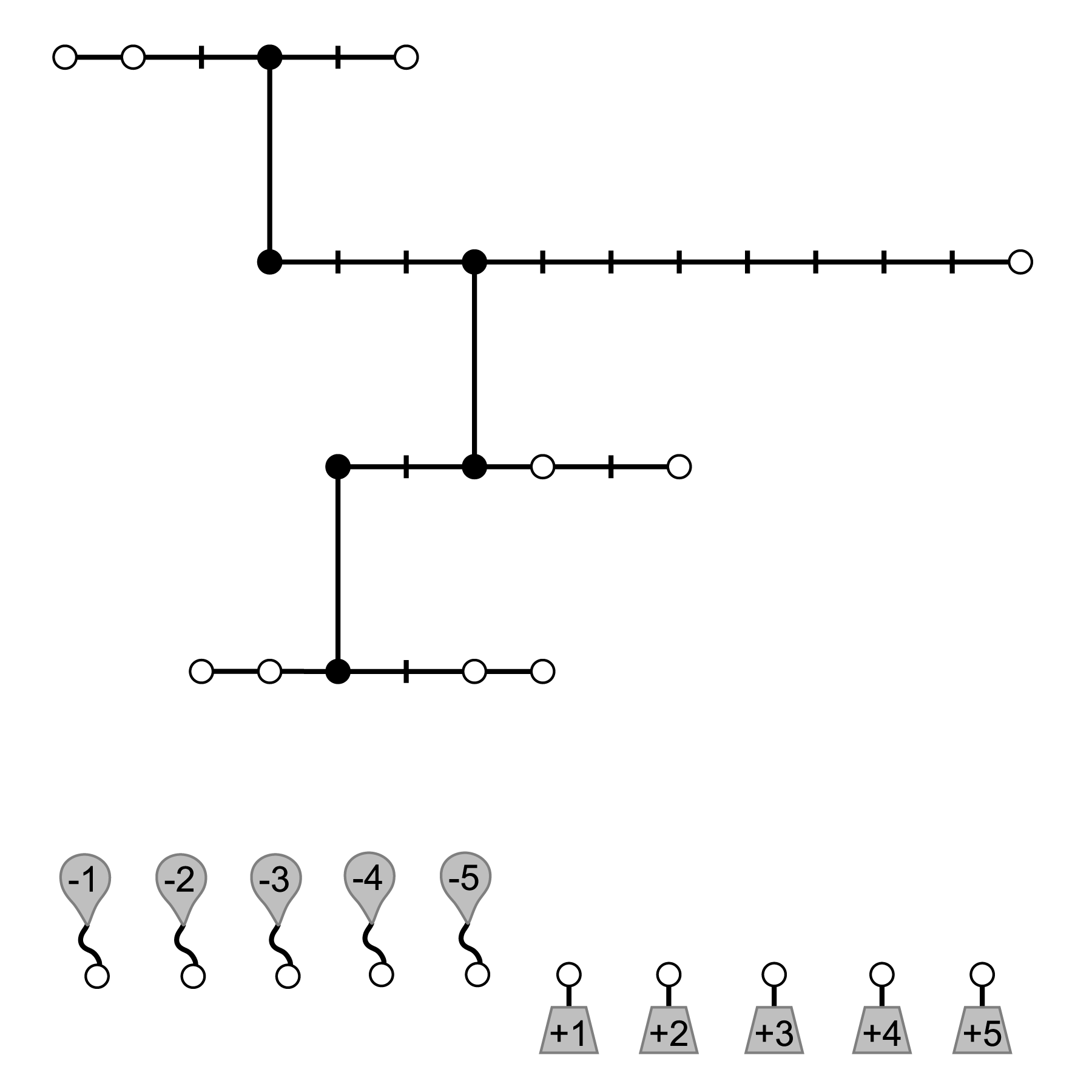
Part VI revived a theme we saw in Utrecht at the 5th WPC--puzzles that required a bit more time to solve, and rewarded inspired thinking rather than just brute force or speed. This is another class of puzzles that I think is valuable, and I hope is used again in future competitions.

I couldn't have been happier with the set of puzzles created by the R&D team at Wizards of the Coast; each of them are worthy of being presented here! However one stands out as being particularly innovative. Balloon Balance was designed by Richard Garfield, the original inventor of the Magic: The Gathering card game. He took the classic balancing puzzle and then removed gravity! Well, almost. What he did do was to remove the top-level fulcrum, and thus remove the orientation of the force of gravity. He then added helium balloons in addition to normal weights, so that some objects pulled up while some pulled down. Once you ignore what seems to be missing and orient yourself properly, it's not as hard as it first seems.

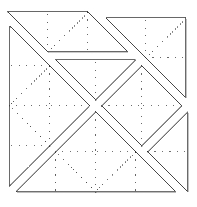
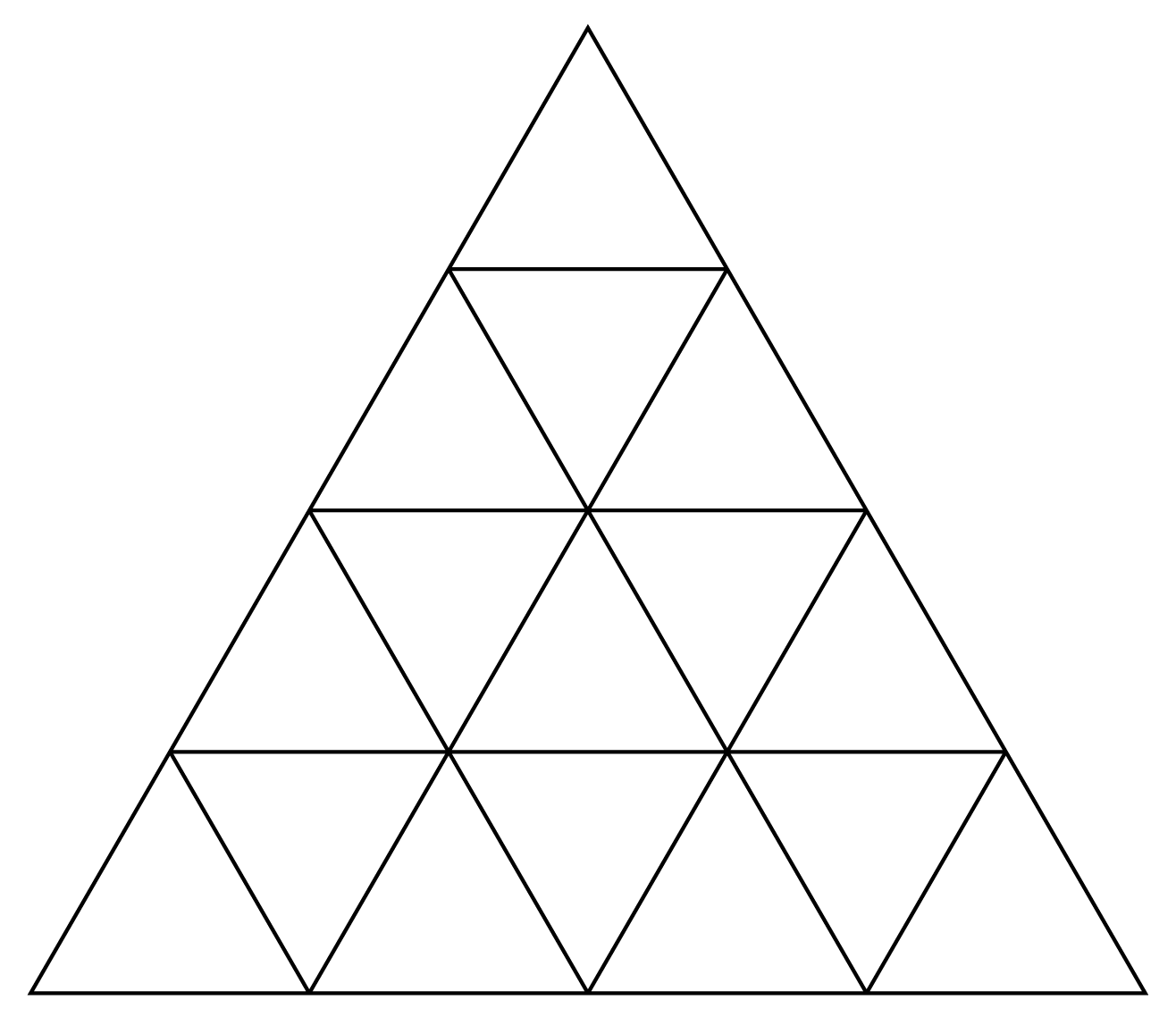
Optimization puzzles, rewarding intuitive solving skills, have appeared in a few recent championships, and I felt this style was worthy of being included again this year as Part VII. However, the original version of Scott Kim's Triangles would have been more a question of accurate counting (and also a disaster for judging), so I decided to limit the search to just equilateral triangles rather than triangles of any shape.

A few of the behind-the-scenes events will further illustrate how awkward this sort of problem can be. Scott's original solution diagram reportedly gave 109 triangles. When testing the original version, I ignored the original solution, finding a better diagram with 123 triangles. This is when I changed the goal and returned the original problem back to Scott for publication in one of his magazine articles. When rechecking the count for this article, I could only get 121; Scott's editors had the same trouble. Wei-Hwa Huang was nice enough to confirm the lower count, but also found a better solution with 127 triangles. Ironically, his new diagram was the same as Scott's original, just with a more accurate count! Upon seeing this result, I tweaked it slightly to improve the maximum even higher.

Here is the original version of the problem. Test your reasoning and intuition skills (if not your counting!), and think about what is most likely to increase the triangle count:

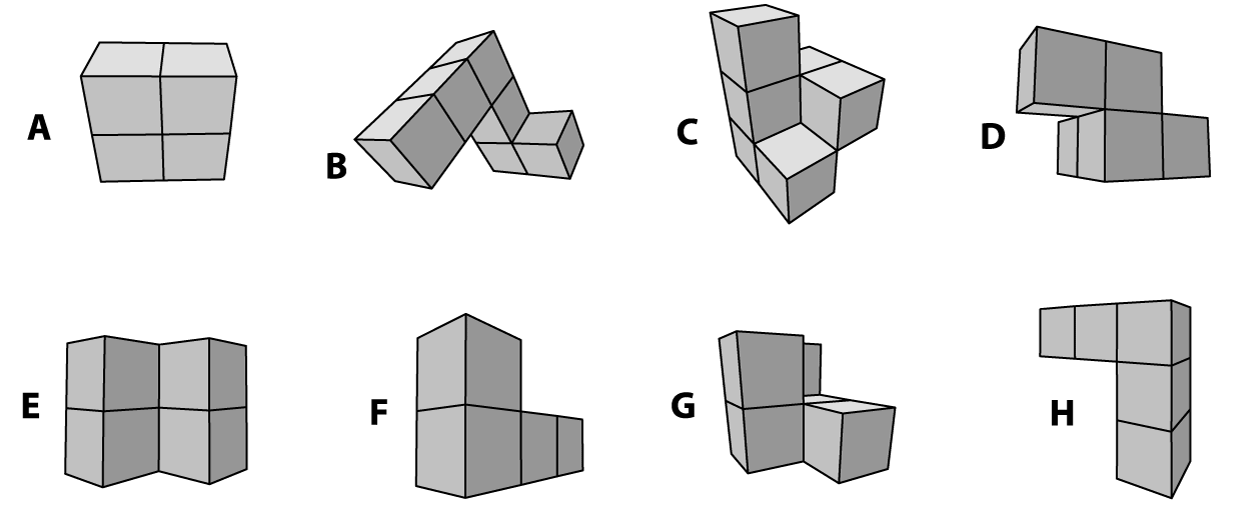
The last round, Part VIII, was another mix of various puzzle types, and included many familiar WPC puzzle styles. Viewpoint is Scott Kim's twist on the classic idea of 3D cube visualization. The original design included 16 figures, but I decided to simplify the puzzle by only using half; we then used the remaining eight figures for the Viewpoint 2 puzzle that appeared in the final round! It turned out well, with each of the separate sets being an appropriate challenge.

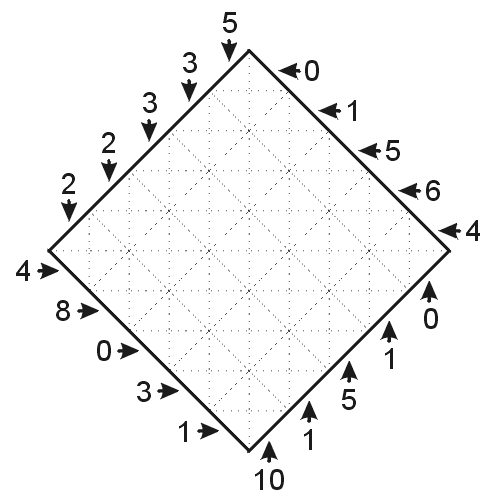
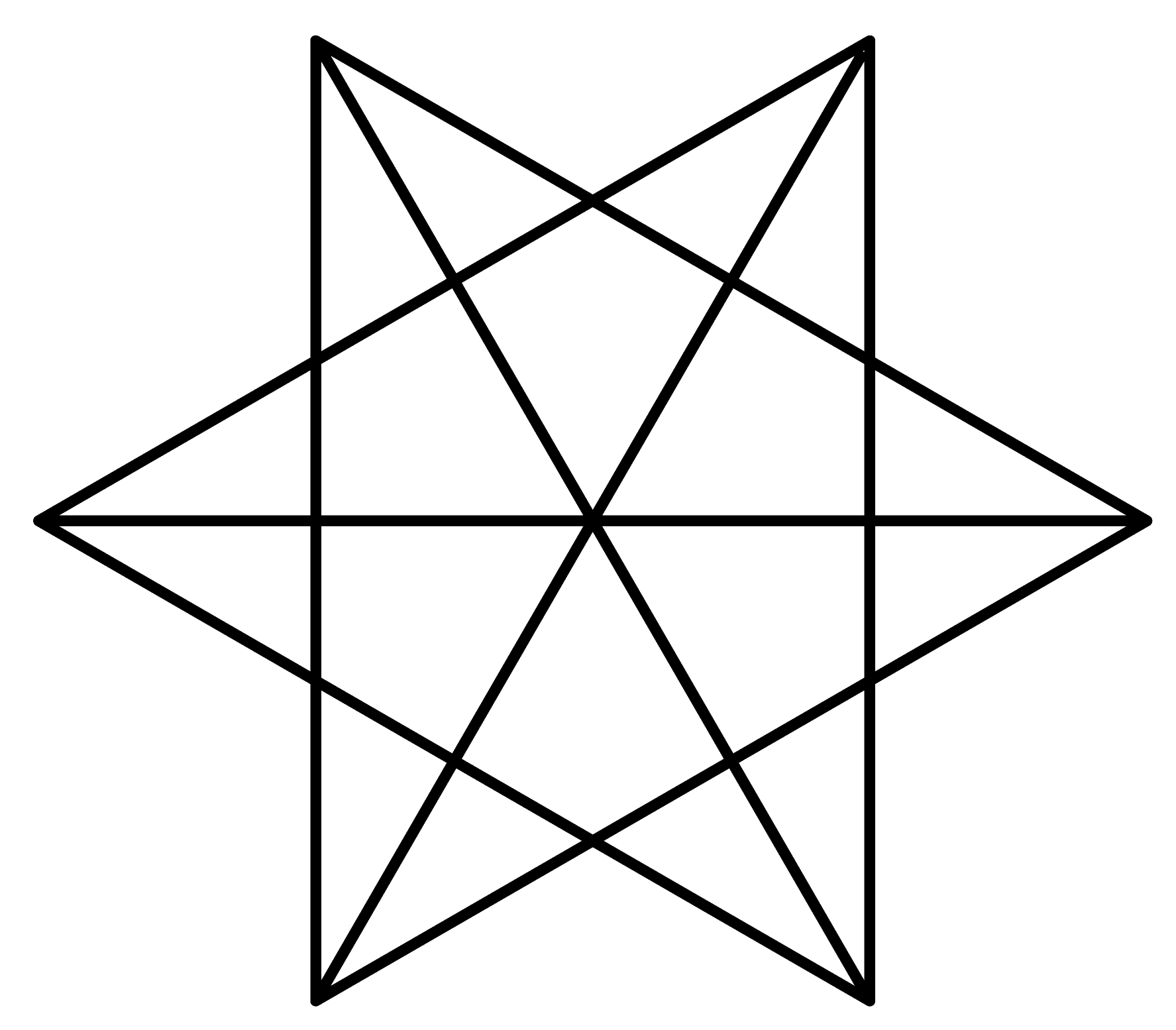
The puzzles used for Part IX, the playoff round, were selected because they were visually appealing, required less than the normal amount of paper work to solve, and still presented a moderate challenge to the finalists. The surprise of the round was definitely the unassuming Triangle counting problem--only 2 of the 10 finalist got this one right, and it was the deciding factor for the individual title. Before you read on, you might take some time now and try solving it for yourself.

There are a number of ways to tackle a problem like this; most are equally valid, but some are significantly more reliable than others. The most typical approach for this type of problem is to determine all the possible triangle shapes, and then determine how many of each type there are. The symmetry of this diagram greatly simplifies the task.

My favorite technique counts the triangle not by shape, but by how many of the 6 star vertices are used. The surprising key observation is that there are NO triangles that don't use one of these six points! The diagram's symmetry further reduces the search space, and the counting turns out to be pretty easy.

Regardless, each technique requires accurate searching and bookkeeping. From talking with a number of the finalists, the most common oversight was missing some of the large triangles that included two vertices.

The competition produced some interesting statistical tidbits. Without editorializing, here are the items that were the most interesting to me:

I hope that everyone enjoyed these puzzles as much as I have. I've had the (un)enviable task of solving each of the puzzles, many of them multiple times. And I'm still not tired of them! I think this is a great tribute to the many designers who contributed their hard work to make the competition a success.

Results

Puzzles