1999
US/Canadian Qualifying Test
1. Four Easy Pieces (5 points)Divide the grid into four contiguous regions, each containing four numbers, such that the total for each region is the same.
Answer key: Enter the four numbers of each region in ascending order. (The order in which you enter the regions themselves does not matter.) |
|
2. Number Maze (10 points)Start at the cell in the upper-left corner (marked "5"). Move horizontally or vertically (but not diagonally) the number of cells indicated. For example, your first move can be down five cells to the 2 or right five cells to the 4. Continue in the same manner in a series of moves from there, always moving the number of cells indicated by your current position. Find the path to the Goal (G) that uses the fewest moves.
Answer key: Enter the numbers visited, in order, from start to finish. |
|
5
|
3
| 3 | 2 | 4 | 4 |
| 3 | 3 | 4 | 4 | 2 | 4 |
| 1 | 4 | 1 | 2 | 4 | 2 |
| 3 | 4 | 1 | 3 | 2 | 3 |
| 4 | 3 | 2 | 2 | 4 | 4 |
| 2 | 3 | 5 | 2 | 3 | G |
|
3. Traffic Jam (10 points)Find the following 20 names of automobile marques in the grid of letters shown. Each name reads in a straight line horizontally, vertically, or diagonally. The central 16 letters in the grid have been removed and are for you to determine.
Answer key: Identify the 16 missing letters in order, reading from left to right, starting with the top line, then the second, then the third, and finally the fourth.
AUDI
AUSTIN
CADILLAC
FIAT
FORD
HUDSON
HYUNDAI
ISUZU
LADA
MASERATI
MAZDA
OPEL
PONTIAC
RENAULT
REO
SAAB
SUBARU
TALBOT
TRIUMPH
YUGO |
|
| I | G | T | N | S | A | A | B | O | F |
| L | E | P | O | U | Z | U | S | I | R |
| H | E | O | S | B | T | I | A | H | C |
| Y | E | T | | | | | C | F | A |
| U | I | S | | | | | O | E | D |
| N | H | P | | | | | T | A | I |
| D | L | E | | | | | T | D | L |
| A | T | N | N | E | R | S | U | A | L |
| I | E | O | G | U | Y | A | O | L | A |
| R | P | A | D | Z | A | M | S | N | C |
|
4. Digitalis (10 points)Each letter from A to I represents a different digit from 1 to 9. Determine which digits correspond to which letters so that the six equations are correct.
Answer key: Give the values for the letters A to I in order. |
|
IFIB
|
-
|
EBG
|
=
|
CEH
|
|
-
|
|
-
|
|
+
|
|
CCE
|
/
|
GD
|
=
|
FE
|
|
=
|
|
=
|
|
=
|
|
EFF
|
+
|
EED
|
=
|
CBA
|
|
5. Perfection (15 points)Fill
each cell with any digit (0-9) so that for the seven multidigit numbers
formed across and down, one is a perfect cube (already filled in for you)
and the rest are perfect squares. Numbers do not begin with the digit 0.
Answer key:
Enter the three missing horizontal numbers. |
|
6. Cartoon Sequence (5 points)The six panels in this cartoon (A-F) have been mixed up. Put them back in their logical order.
Answer key: List the six letters in order.
7. Balancing Act (15 points)Assign the values 1 to 10 to the weights in the diagram so that everything balances as shown. Each number will be used exactly once.
Answer key: List the numbers in order from left to right.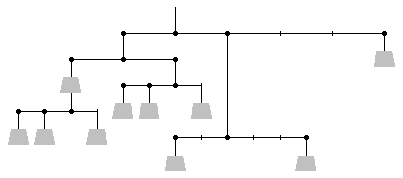
8. Snake in the Grass (15 points)Find
a path from the start (S) to the goal (G), moving horizontally or vertically
from square to square. The path cannot go through the numbered squares, and will
never loop back to touch itself, even diagonally. (For example, this means that
a 2 x 2 area can never be completely used by the path.) A number indicates how
many squares of the path touch -- including diagonally -- that numbered
square. The S and G cells are part of the path. Ignore the highlighting of the
gray rows for the solving of the puzzle; they are used for the answer key.
Answer key:
Enter the number of cells used by the path in each of the five highlighted rows,
from top to bottom.
| | | |
5 | S |
| | | | | | |
| | | | | | | | | | |
6 |
|
| | | | | | |
1 |
| | | | |
| | | | | | | | | | | | |
| | | | | | | | | | | | |
| |
2 |
| | | | | | | | | |
| | | | |
1 |
|
1 |
|
4 |
| | |
| | | | | | | | |
3 |
| | |
| 4 |
| | | | | | | | | | |
| | | | | | | | | | |
2 |
|
| | | | | | |
4 |
|
4 |
| | |
| | | | | | | | | | | | |
| | | | | | | | | | |
7 |
|
| G |
|
4 |
| | |
3 |
| | | | |
| | | | |
3 |
| | | | | | |
| |
4 |
| | | | | | | | | |
9. Rule of 72 (15 points)Place the numbers from 1 to 9 in the blanks to make the equation correct. Each digit will be used exactly once. Operations are to be performed strictly from left to right. All intermediate results are whole numbers.
Answer key: Enter the digits in order from left to right.
__ - __ / __ + __ / __ +
__ / __ x __ - __ = 72
10. A Change for the Bettor (5 + 10 points)
5 points for part 1; 10 points for part 2. Note: separate penalties apply.
How much money can you have in $1, $2, $5, $10, $20, and $50 bills and still not be able to make change for a $100 bill?
Answer Key 10.1: Enter the dollar amount.
Suppose that in an alternate universe the dollar bill is worth 60 cents, and there are coins in three different denominations, not necessarily cents, nickels, dimes, etc. You know that the most change you could have in that universe and still not be able to make change for a dollar is 2 dollars and 13 cents (i.e., 133 cents). What are the three denominations of coins?
Answer key 10.2: Enter the three values.
11. C Hunt (10 points)Which four numbers add up to exactly 100?
Answer key: Enter the four numbers in ascending order. |
|
12. Pentomino Paint by Numbers (15 points)Place the twelve unique pentomino shapes (shown below) in the white 12 x 12 grid so that no two shapes touch each other, even diagonally. The shapes can be rotated and/or reflected. The numbers outside the white grid indicate the sequence and size of consecutive cells used by the shapes in the corresponding row or column. For example, the clue for the fourth row is 2,3. This means two consecutive cells are black, followed by three consecutive black cells, separated by at least one empty cell -- there may be empty cells before and/or after the groups of black cells.
Answer key: Enter two groups of letters. The first group contains the letters of the pieces that required reflection (relative to the bottom diagram), when placed into the grid. The second group contains the letters of the pieces that appear in the grid with the same orientation as shown in the bottom diagram.
| | | | 1 | | 2 | | 2 | | | | | |
| 1 | | 1 | 2 | 2 | 1 | 1 | 2 | | 1 | 1 | 3 |
| 5 | 3 | 2 | 1 | 1 | 1 | 1 | 3 | 2 | 1 | 3 | 1 |
| 1 | 1 | 2 | 1 | 1 | 1 | 2 | 1 | 1 | 1 | 2 | 2 |
| | 1 | 3 | 3 | | | | | | | | | | | | |
| 3 | 1 | 1 | 1 | | | | | | | | | | | | |
| | 1 | 1 | 1 | | | | | | | | | | | | |
| | | 2 | 3 | | | | | | | | | | | | |
| 1 | 3 | 1 | 2 | | | | | | | | | | | | |
| | | 1 | 1 | | | | | | | | | | | | |
| 1 | 4 | 1 | 2 | | | | | | | | | | | | |
| | 1 | 1 | 1 | | | | | | | | | | | | |
| | | 1 | 3 | | | | | | | | | | | | |
| | | 2 | 1 | | | | | | | | | | | | |
| | 3 | 1 | 2 | | | | | | | | | | | | |
| | | 4 | 2 | | | | | | | | | | | | |
| | N | N | N | | V | V | V | | I | I | I | I | I | | | F | | T | T | T | | |
| N | N | | | | | | V | | | | | | | | F | F | | | T | | | |
| | | | | W | W | | V | | | X | | | | | | F | F | | T | | L | |
| P | P | | W | W | | | | | X | X | X | | Z | Z | | | | | | | L | |
| P | P | | W | | | | Y | | | X | | | Z | | | U | | U | | | L | |
| P | | | | | Y | Y | Y | Y | | | | Z | Z | | | U | U | U | | L | L | |
13. Dem Bones (15 points)A full set of 21 dominoes has been placed in a 7 x 6 rectangular tray. The layout is shown with the pips replaced by numbers, and the domino edges removed. Reconstruct the missing edges.
Answer key: Enter the dominoes that are oriented horizontally in order, reading from left to right, starting with the top row, then the second row, then the third, etc. |
| 2 | 4 | 6 | 4 | 5 | 2 | 5 |
| 4 | 1 | 2 | 1 | 3 | 2 | 5 |
| 4 | 1 | 6 | 3 | 3 | 2 | 6 |
| 5 | 6 | 6 | 1 | 4 | 3 | 6 |
| 3 | 1 | 5 | 1 | 1 | 2 | 3 |
| 5 | 6 | 2 | 3 | 5 | 4 | 4 |
|
|
14. UFO #1 (10 points)
15. UFO #2 (20 points)
| |
Each
letter represents a rocket ship that travels horizontally or vertically,
but only directly toward another ship -- as far as it can go without
hitting it. One move is a continuous sequence of such traverses
made by the same ship. In the example below, the first move could be ship
X moving south to D, then east to C, north to A, and finally west to B.
X's first move could also end anywhere along the way. Neither A, B, nor C
can make the first move because there is no ship that any one of these can
move toward. The goal is to end up with ship X on the center space after
six complete moves.
Example:
Answer key: Enter the six moves that get X to the center space. Describe each move with the name of the rocket and the directions traveled. In the example problem, the three-move solution is D-NE, A-S, X-E. |
16. Hex Aspiration (20 points)Find a looped path through the diagram subject to the following constraints. The path proceeds from one cell to an adjacent cell, passes through no cell more than once, does not go through any numbered cells, and never makes a sharp-angled turn (i.e., a turn at a 60° angle). Each number indicates how many of the adjacent cells are part of the path.
Answer key: Indicate which of the cells in the gray diagonal are part of the path. Use a 1 to indicate that the path goes through a cell; use a 0 to indicate that the path does not go through a cell. List the 11 digits in order from SW to NE. Your entry will look something like "10011101000". | 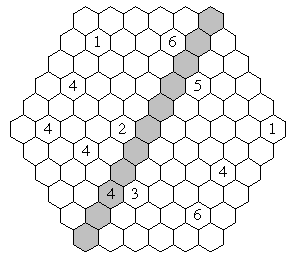 |
17. Battleships #1 (10 points)Locate the position of the 10-ship fleet (one battleship, two cruisers, three destroyers, and four submarines, as shown in the legend) in the grid. Each segment of a ship occupies a single cell. Ships do not touch each other, even diagonally. The numbers on the bottom and right edges of the grid reveal the total number of ship segments that appear in each respective row or column. Cells with water (indicated by tildes) do not contain ships. (For solving, ignore the letters and numbers on the top and left edges.)
Answer key: Enter the location of the four submarines (i.e., the single-segment ships). Use the coordinates on the top and left edges to specify their places. For example, the given water locations are A4, F1, and H4. |
| | A | B | C | D | E | F | G | H | I | |
| 1 | | | | | | ~ | | | | 2 |
| 2 |  | | | | | | | | | 2 |
| 3 | | | | | | | | | | 3 |
| 4 | ~ | | | | | | | ~ | | 2 |
| 5 | | | | | | | | | | 2 |
| 6 | | |  | | | | | | | 1 |
| 7 | | | | | | | |  | | 5 |
| 8 | | | | | | | | | | 1 |
| 9 | | | | | | | | | | 2 |
| | 4 | 0 | 3 | 2 | 2 | 2 | 1 | 4 | 2 | |
|
Battleship
    | Destroyers
      | Cruisers
      | Submarines
    |
18. Battleships #2 (15 points)Same rules as for Battleships #1 (above) except: Some of the numbers on the bottom and right edges are missing. These are for you to determine.
Answer key: Same as #17. |
| | A | B | C | D | E | F | G | H | I | |
| 1 | | | | | | | | | | 3 |
| 2 | | | ~ | | | | | | | |
| 3 | | | | | | | ~ | | | 2 |
| 4 | | | ~ | | | | | | | |
| 5 | | | | | | | | | | |
| 6 | | | | | | | | | | 6 |
| 7 | | | | | | | | | | |
| 8 | | | | | | | | | | |
| 9 | | | | | | | | | | 1 |
| | | 1 | 6 | | 1 | | 5 | 1 | 5 | |
|
Battleship
    | Destroyers
      | Cruisers
      | Submarines
    |
19. Name Dropping (15 points)Thirty-two of the 33 people's names listed below can be inserted in the grid, reading in regular crossword fashion (across and down). One name (RABIN) has been put in to get you started.
Answer key: Enter the extra name.
AESOP
ANDRE
ASSAD
COSBY
DONNE
DUPRE
ERNST
GATES
GILES
HEARN
HENIE
HEROD
KLEIN
LEARY
LENIN
MARTI
NEHRU |
NIOBE
OAKES
PAINE
PEPYS
POTOK
RABIN
RUSSO
SATIE
SILLS
SNEAD
STERN
STYNE
SYNGE
TRIBE
TWAIN
UNSER |
|
 |
20. Laser Tag (15 points)74,088 transparent plastic cubes are painstakingly cemented together, face to face, to create a solid rectangular box whose dimensions are 63 x 42 x 28. A laser is beamed from one corner of the box to the diagonally opposite corner. Through the interior of how many cubes does the beam pass?
Answer key: Enter the number of cubes.
21. Cross Sums Typo (15 points)This is a standard Cross Sums puzzle, except that three clues have been removed. A single digit (1 to 9) goes into each white square. A clue number represents the sum of the digits to be placed in the squares to the right of it (for an across answer) or beneath it (for a down answer). No digit is repeated within an answer. Determine the values of the missing clues (marked A, B, and C) in order to complete the grid.
Answer key: Enter the missing clues in the order A, B, C.
22. Absolutely Dotty (20 points)Draw
a single continuous loop by connecting neighboring dots horizontally or
vertically (but not diagonally). A numbered square indicates exactly how many of
its four edges are used by the path.
Answer key: For each of the 11
dots in the middle row reading left to right, and for the 11 dots in the middle
column reading top to bottom, indicate the direction that the path takes through
that dot. Use "O" for no path, "L" for a 90� turn in any
direction, and "I" for a straight path in either direction. Your entry
will look something like "OIILOOLLIOO OOILLOOLIIO".
23. Letter Bourse #1 (10 points)Enter the letters A, B, C, D, E once in each row and column. The clues outside the grid indicate which letter appears first from that direction. In the first puzzle, for example, D must be the leftmost letter in both the first and third rows, and C must be the bottommost letter in the first and second columns.
Answer key: Enter the five letters in order (from left to right) in each row, starting with the top row, then the second row, then the third, etc. |
| | | B | B | | D | | | |
| D | | | | | | | | C |
| A | | | | | | | | C |
| D | | | | | | | | |
| | | | | | | | | B |
| A | | | | | | | | E |
| | | | | | | | | E |
| | | | | | | | | |
| | C | C | E | | B | D | | |
|
24. Letter Bourse #2 (10 points)See instructions for the previous problem, Letter Bourse #1.
Answer key: Same as #23. |
|
25. Rolling Die Maze (20 points)
20 points for the
shortest path; 10 points for a non-minimal solution under 50 moves.Place
a standard six-faced die on the Start square with the 6 on top (the 1 will lie
directly on the paper). For each move, roll the die once horizontally or
vertically to an adjacent white square. (After the first move, the 6 will be on
the face farthest from the Start square; the 1 will be closest.) Do not
otherwise rotate the die between moves. There is one special restriction: The 1
can never be on top (including at the Goal). Find the shortest route
from Start to Goal, or any path with under 50 moves.
Answer key:
Enter the total number of moves followed by the directions traveled (N,E,S,W) in
reaching your solution.
26. Crossing Hungary (30 points maximum)
Open-ended
challenge with partial scoring: 3 points for 10 words, 5 points for 11, 8 points
for 12, 12 points for 13, 17 points for 14, 23 points for 15, and 30 points for
all 16 words. No penalty for errors.Below are the names of 16 Hungarian cities and towns. Arrange as many of them as you can reading across and down in a 9 x 11-square grid so that they interlock as on a standard Scrabble® board or crossword. Two letters cannot abut each other unless they are part of one of the names. No part of the completed interlock can be completely separated from the rest. Diacritical marks should be ignored.
Answer key: Enter the number of cities used, followed by the solution itself, line by line. Use spaces ( ) to indicate the unused cells.
CEGL�D
CSORNA
ERCSI
KALOCSA
KECEL
LENTI
MAK�
M�LYK�T
M�R
�ZD
SIKL�S
SZEGED
TAM�SI
TAPOLCA
TURA
ZIRC |
|
|